Tři zdroje a tři součásti geometrizujících vizí Ladislava Daňka

Přírodovědecká fakulta Univerzity Palackého, Olomouc

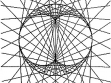
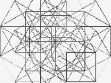
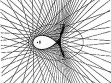
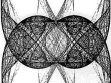
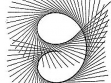
Ladislav Daněk (nar. 1958) je uznávaný olomoucký výtvarník a respektovaný teoretik umění. Pro základní charakteristiku jeho tvorby se odvolejme na povolanější. Následující tři citace dostatečně reflektují podstatu a nezaměnitelnost Daňkova rukopisu:

„Geometrie, geometrie, geometrie. To je kresba Daňka. Stovky hodin strohého rýsování tužkou na konstruktérském milimetrovém papíře, jehož pravidelný pravoúhlý rastr slouží jako podklad pro novou, jinak strukturovanou geometrickou síť. I maximální přísnost v dodržování geometrické výstavby i omezení vlivu drobných odchylek daných zachvěním ruky však přinášejí někdy až překvapivě lyrický vjem. Shluky světelných a temných bodů vyvolávají iluzi těkavého chvění, které je navíc prozářeno vnitřním světlem vystupujícím z kresby. Neosobní rýsování je zdrojem citového zážitku - není to důkaz nad důkazy, že sám výtvarný řád tohoto typu práce má svůj vlastní život s bohatými možnostmi sdělení?! Jako by autor nebyl objevitelem, ale pouhým služebníkem, který je povolán k tomu, aby zprostředkoval poselství, které již někde existovalo. Jedině on však ví kde. Jedině on je schopen potlačit různé estetizující výtvarné choutky, aby pouze a jedině onen strohý systém mohl promluvit svou nečekaně rozmanitou řečí.“
(Radek Horáček v katalogu výstavy „Ladislav Daněk, Vladimír Havlík, Petr Jochmann, Inge Kosková“, Galerie Na Skořepce, Brno, 5. 4.–3. 5. 1991)

„Výslednou kresbu vnímáme jako pole, tvořené různou intenzitou linií, uzlových bodů, interferencí, ale také jako vlnění či chvění, zhušťování a zřeďování, tedy jako dynamickou plochu, ovládanou svými vlastními zákony.“
(Jiří Valoch v katalogu výstavy „Ladislav Daněk. Kresby“, Galerie Pod podloubím, Olomouc, 17. 10.–5. 11. 1987)

„Ladislav Daněk utkal barevné fluidum ze stovek čar do zelené osnovy silového pole. Usilovně a stále hledal světlo, které rezonuje v hlubinách nekonečna. Nachází jej v harmonii přísného geometrického řádu a v zá- vratném působení energetických shluků. Trpělivým spojováním a křížením kosmických drah prorýsoval roztěkanému zraku cestu k mystickému transcendentnu.“
(Yvonna Boháčová v katalogu výstavy „Zapomenuté světlo“, Ladislav Daněk, Vladimír Havlík, Václav Stratil, Sovinec, Kostel sv. Augustina, 5. 9.–28. 10. 1992)

Nejvýraznějšího efektu tedy dosahuje Daněk tím, že aplikací výhradně lineárních elementů vytváří nelineární struktury (často na způsob negativu), včetně dynamických a optických iluzí. Spíše než další výklad či rozvíjení podobných myšlenek, avšak převážně v matematických termínech, bude naší snahou a hlavním cílem začlenění Daňkovy tvorby do širšího – přírodovědného kontextu. Přitom budeme chtít poukázat na následující tři zdroje a tři součásti jeho geometrizujících vizí:

zdroje:
• kombinatorika a její vizualizace (v historické posloupnosti: Raimund Lullus g Athanasius Kircher, S. J., g ... g architektura neuronových sítí),
• obálky (anglicky: envelopes, německy: Einhüllenden, rusky: ogibajuščije) křivek,
• světelné kaustiky (optické katastrofy);

součásti:
• lineární elementy (úsečky) na milimetrovém papíře (převážně tužkou, ale také barevnými pastelkami a někdy i fixy),
• světelné efekty,
• jednoduchý rytmus (symetrie + dynamika).


1. Mundus combinatus
„Otec Kircher prostudoval všechny traktáty o kombinatorice, Lullem počínaje, tady vidíte, co pak otiskl ve své knize Ars Magna Sciendi…‘
»Připomíná to háčkovanou dečku,« poznamenal Belbo.
»Kdepak, můj milý, jsou to veškeré možné kombinace n prvků. Souhrnný výpočet, přesně jako v Sefer Jecira. Výpočet kombinací a permutací, podstata Temury!« “
Tuto příznačnou ukázku z erbovního románu postmoderny Foucaultovo kyvadlo (viz [E1, str. 515]) dokládá jeho autor Umberto Eco dobovou ilustrací (viz obr. 1), převzatou z kombinatorické knihy Ars magna sciendi, vydané v Amsterodamu r. 1669, od Athanasia Kirchera, S. J.. Ten vyšel a důsledně (někdy až do absurdna) rozvinul metodu Raimunda Lulla z jeho Ars generalis ultima z r. 1303, nazývané podle štrasburského vydání z r. 1598 rovněž Ars magna et ultima. Užití permutací, variací a kombinací nesloužilo oběma pouze k technickému zvládnutí problémů (např. na obr. 1 se počet spojnic rovná počtu dvoučlenných variací s opakováním z 18 prvků, tedy V(2,18) = 182 = 324 úseček), nýbrž – poněkud ambiciózně – zejména při procesu „objevování“ k vymezení možných scénářů. Tento způsob uvažování byl pro – nejen exaktní – barokní vědu typický. Zájemce o tuto pro- blematiku odkazujeme na krásnou monografii Thomase Leinkaufa Mundus combinatus [L], jejíž titul posloužil symbolicky pro název tohoto oddílu.

Zmíněná ilustrace je právě takovým příkladem aplikovaného kombinatorického scénáře. 18 ekvidistantně uspořádaných znaků je zrcadlově (symetricky) zdvojeno na vertikálách, přičemž přípustné relace (zde každý znak s každým, včetně se sebou samým) jsou vyjádřeny prostě tak, že znaky v relaci se spojí úsečkou. V teorii grafů (viz např. [H]) se příslušný objekt značí K18,18. Tento mechanický způsob lze snadno zvládnout s užitím počítače; výsledná vizualizace však postrádá – na rozdíl od mědirytiny z obr. 1 – estetický náboj a lyrickou rozechvělost (viz obr. 2).
Dopad obou Ars magna na další vývoj exaktní přírodovědy byl značný. Dvacetiletý Gottfried Wilhelm Leibniz napsal pod jejich vlivem Dissertatio de arte combinatorica, vydané v letech 1875-1890. Jak však poznamenává Eco v [E2, str. 243], zatímco Lullus (a potažmo Kircher) vědomě omezil počet termínů a z teologicko-rétorických důvodů byl připraven mnohé kombinace zavrhnout, protože by vytvářely nepřípustné věty, Leibniz se naopak zajímá o tvůrčí logiku, v níž může kombinacemi generovat dosud neznámé světy.

„A vytvořit abstraktní model všech možných kombinací, to je jedna věc, a druhá věc je vymyslet stroj, který by všechny tyto kombinace beze zbytku vykonal. Jak Kircher, tak jeho žák Schott se proto vrhli na vymýšlení mechanických kolovrátků, přístrojů založených na jakýchsi děrných štítcích, computerů ante litteram, založených na binárním výpočtu. Zkrátka kabala aplikovaná na moderní mechaniku.“

Takto pokračuje o několik řádků dále úvodní citát (viz opět [E1, str. 515]). A vskutku, jestliže ne ještě od Kirchera, pak jistě již od Leibnize to není k počítačům až tak daleko. V současnosti jsou jedním z největších hitů informatiky tzv. neuronové sítě. Přitom jde do značné míry o renesanci myšlenek (v novém kontextu) otců informatiky Alana Turinga, Johna von Neumanna, Norberta Wienera, aj. Analogie mezi strukturou a činností mozku a počítače resp. neuronových sítí je nabíledni. O některých klíčových pojmech jako jsou bio-logika, (mnohovrstvý) perceptron (MLP), Hopfieldova síť, atd. je populárně pojednáno například v 5. kapitole knihy [CH]. K úvodu do dané problematiky může posloužit např. kniha [MRS]. Z našeho hlediska je podstatné, že architektura neuronových sítí vykazuje podobné vnější znaky jako výše uvažované kombinatorické struktury (viz obr. 3). Spojnice jsou zde vedeny mezi interaktivními výpočetními elementy – v terminologii neuronových sítí nazývanými neurony. Kromě bezpočtu aplikací (včetně strategických) mají neuronové sítě velkou přednost v odolnosti vůči selhání. O dalších možnostech aplikované kombinatoriky – včetně jednoduchých vizualizací – se je možné dočíst např. v [Kf].


2. Nelinearní struktury
Uvažujme nyní jednoparametrickou množinu křivek (např. úseček - viz. obr. 4) v rovině. Obalová křivka, která se všech těchto křivek dotýká, se nazývá obálka. Přitom se předpokládá, že křivky z jednoparametrické třídy nemají tzv. singulární body. Matematičtěji: Je-li na množině W × P Ě R2 × R, kde P Ě R je interval, dána spojitá funkce F(x,y,p) se spojitými derivacemi F/ p, 2F/ p2, přičemž 2F/p2 0, pak křivky určené rovnicí F(x,y,p) = 0 tvoří jednoparametrickou soustavu. Jestliže pro každou hodnotu parametru p Î P určují rovnice F(x,y,p) = 0 a F/p = 0 bod, pak jej nazveme charakteristickým neboli mezním bodem soustavy křivek F(x,y,p) = 0. Je-li dále možno z rovnic F(x,y,p) = 0 a F/p = 0 eliminovat parametr p a je-li výsledek této eliminace dán rovnicí G(x,y) = 0, která implicitně definuje křivku, pak se tato křivka nazývá obalová křivka (obálka) soustavy F(x,y,p) = 0. V každém charakteristickém bodě [x0, y0, p0] Î W × P, pro který 2F/p2 ą 0, (a který je regulárním bodem obalové křivky), se obalová křivka dotýká příslušné křivky soustavy. Jinými slovy: obě křivky mají v takovém bodě společnou tečnu. Typickým příkladem obalové křivky je parametricky zadaná funkce x = – g˘ (p), y = – p g˘ g (p) + g(p), která je tzv. singulárním řešením neboli singulárním integrálem známé Clairautovy diferenciální rovnice y = px + g(p), kde p = dy/dx. Tuto obálku obalují přímky určené obecným řešením Clairautovy rovnice (viz např. [Km]). Zcela analogicky lze definovat obalovou plochu pomocí jednoparametrické třídy ploch určených rovnicí F(x,y,z,p) = 0.
Příkladem obálek jsou evoluty (obálky normál), kaustiky (o nichž ještě bude řeč v příští části), ortonomiky (viz obr. 5), antiortonomiky (viz. obr 6), ale i zdánlivě mnohem méně matematické objekty, jako např. okraj požáru na poli nebo zmíněná háčkovaná dečka z úvodního citátu předchozí části. Existují totiž další (alternativní, viz např. [BG]) definice obálky jakožto limity průniku sousedních křivek z jednoparametrické třídy nebo (nahlédnutelněji) jakožto hranice oblasti zaplněné jednoparametrickou třídou křivek. Teorii obálek je věnována celá monografie [Z].

K vytvářecím křivkám kontur lze překvapivě dojít i v rámci teorie fraktálů (viz [A], [AF]). Zde jsou ovšem vytvářecí křivky definovány implicitně jakožto invariantní množiny tzv. Hutchinson-Barnsleyova zobrazení generovaného pomocí iteračních funkčních systémů (IFS). Invariantní množina neznamená, že by všechny její body byly pevné, tj. zobrazující se samy na sebe, avšak z dané množiny již při iteracích neuniknou.
Příkladem takové invariantní množiny je tzv. topologický fraktál (viz [AF]) na obr. 7, jehož generující diskrétní dynamický systém tvoří funkce tvaru :

f1(x,y) := (cos(x2/2 + y2/2), sin(x2/2 – y2/2)),
f2(x,y) := (1 – cos(x2/2 + y2/2), sin(x2/2 – y2/2)),
f3(x,y) := (cos(x2/2 + y2/2), 1 – sin(x2/2 – y2/2)),
f4(x,y) := (1 – cos(x2/2 + y2/2), 1 – sin(x2/2 – y2/2)),

Hutchinson-Barnsleyho zobrazení je pak jednoduše definováno jako

F(x,y):=Ufi (x,y), (x,y) Î R2.

Označíme-li tedy topologický fraktál z obr. 7 jako F, platí F(F ) = F. Pro detekci hranic atraktorů diskrétních dynamických systémů a jejich oblastí přitažlivosti lze někdy aplikovat s podobným efektem tzv. kritické křivky (viz. článek [AD], ve kterém je velká pozornost věnována algoritmům pro softwarovou simulaci).

Další možnost představují rovinná zobrazení (dvojrozměrné projekce) vícerozměrných polytopů. Polytopy jsou geometrické objekty ohraničené částmi přímek (v 2D), rovin (v 3D) a nadrovin (v 4 a více D). V rovině se polytopy nazývají polygony a v prostoru mnohostěny. Jonathan Bowen vytvořil v r. 1981 program pro znázornění vícerozměrných krychlí v rovině (viz www.jpbowen. com/publications/ndcubes.html). Na obr. 8 je znázorněna šestirozměrná a na obr. 9 desetirozměrná krychle.

H. S. M. Coxeter dále zobecnil v knize [C] regulární polytopy na tzv. regulární komplexní polytopy podobně, jako se mají komplexní čísla k reálným. Na obr. 10 a 11 leží uzlové body vytvářecích úseček Coxeterových regulárních komplexních polytopů na soustředných kružnicích.
Objekt na obr. 7 je – podobně jako na Daňkových kresbách – strukturovaný. Kontury zde tvoří – na rozdíl od Daňkem výhradně užívaných úseček (viz. rovněž obr. 4, 6, 10, 11) nebo křivek pouze jednoho druhu (např. kružnic na obr. 5) – celá škála křivek. Přestože tedy byly vytvářejícími křivkami často – u Daňka výhradně - pouze úsečky (viz obr. 4, 6, 10, 11), jsou vzniklé struktury (obálky) – s jedinou výjimkou dvou vertikál na obr. 7 – nelineární.

Podobně jako u Daňka je na obr. 7 dosaženo delikátního efektu pomocí iluzorního jednoduchého rytmu, vzniklého kombinací symetrie a dynamiky (neregulárnosti) obálek (kaustik). Této problematice se věnuje monografie [FG] s mnoha krásnými ilustracemi.


3. Budiž světlo
Jak jsme se již zmínili v předchozí části, jsou významným (fyzikálním) příkladem obálek tzv. světelné kaustiky (kaustika např. vzniká, když položíme na podložku ozářený prsten, lze ji pozorovat i v šálku čaje). Představme si světelné paprsky vycházející současně ze všech bodů g(I) ve směru normál, kde g : I g R2 je planární křivka s jednotkovou rychlostí. Pak g(I) nazveme výchozí vlnovou frontou a křivku, na níž „vzniká“ (vytváří ohniska) světlo – kaustikou. Světelná ohniska vznikají tam, kde se protínají nekonečně blízké normály – viz obr. 12, kde kaustika vznikla při odrazu svazku paralelních paprsků od kružnice.
Poněvadž kaustiky nejsou nic jiného než světelné obálky, na nichž intenzita světla vzrůstá „skokem“, můžeme je rovněž uvažovat v rámci teorie katastrof (viz [A], [AK]), jejímiž zakladateli jsou René Thom, Vladimír I. Arnol’d a Erik C. Zeeman, jako tzv. elementární optické katastrofy. Tento nápad pochází od profesora univerzity v Bristolu Michaela V. Berryho, který sám optické katastrofy simuloval (a to s nevšedním estetickým výsledkem – viz [B], [BU]) difrakcí laserového paprsku na různých površích.
I my jsme se před časem pokusili o podobnou simulaci pomocí jednoduše sestavených optických soustav pro pozorování, jejichž základ tvořily čočky s vhodnými aberacemi a dále objektiv, matrice a stínítko (viz [AK]). Jako výchozí obraz jsme na stínítku pozorovali řez svazkem ve tvaru koule. Při pohybu čočky podél optické osy se průměr koule měnil a při pohybu napříč osy se obraz koule otáčel týmž směrem, což vyvolávalo dojem, jako by se celá koule otáčela v prostoru. Při natáčení čočky vůči ose svazku laseru se z hrotu začal vytvářet komatický obláček, přičemž interferující skvrny „stékaly“ z koule do hrotu a z hrotu do obláčku. Velmi zajímavé kaustické kompozice jsme získali při průchodu laserového svazku tvarově hůře definovanými prostředími jako kapkami vody, bublinami, apod. Podstatné rovněž bylo, v jak velkých vzdálenostech za vytvářejícím náhodným prostředkem jsme jednotlivé řezy kaustik pozorovali. V článku [AK] je celý postup podrobně popsán a zdokumentován pěti černobílými fotografiemi. Na obr. 13 je možno rozeznat celou plejádu optických katastrof, zatímco na obr. 14 vytváří kaustiky katastrofu typu „motýlek". Citované práce [B], [BU] obsahují alba nádherných fotografií takto simulovaných kaustik.

Důraz na význam světelných efektů u Daňka dokládá i to, že ústředním mottem jeho olomoucké výstavy v Divadle hudby roku 1990 byl citát z Jakuba Demla: „Světlo tak pomalu se rodí jako krystaly.“ Dodejme, že podle Demlova druha Otokara Březiny „Světlo zaniká jen příchodem ještě VĚTŠÍHO světla.“

Literatura:
[A] J. Andres: O nové přírodovědě a nutnosti nové přírodní filosofie. Českoslov. časopis pro fyziku 46,1 (1996), 42–50.
[AD] J. Andres and Z. David: Basin of attraction metamorphoses for two-dimensional endomorphisms. Acta Univ. Palacki. Olomouc, Fac. rer. nat., Phys. 35 (1996), 221-251.
[AF] J. Andres and J. Fišer: Metric and topological multivalued fractals. Int. J. Bifurc. Chaos 14,4 (2004), 1277–1289.
[AK] J. Andres a V. Křesálek: Katastrofy, chaos a krize v optice. Jemná mechanika a optika 10 (1987), 307–310.
[B] M. V. Berry: Singularities in waves and rays. In: „Physique des Défauts 25“ (ed. R. Bahan et al.), North – Holland, Amsterdam, 1981.
[BU] M. V. Berry and C. Uptstill: Morphology of caustics and their diffraction patterns.
In: „Progress in Optics 18“ (ed. E. Wolf), North - Holland, Amsterdam, 1980.
[BG] J. W. Bruce and P. G. Giblin: Curves and Singularities. A Geometrical Introduction to Singularity Theory. Cambridge Univ. Press, Cambridge, 1984.
[C] H. S. M. Coxeter: Regular Complex Polytopes. Cambridge Univ. Press, Cambridge, 1974; druhé vydání: 1991.
[CH] P. Convey and R. Highfield: Mezi chaosem a řádem. Hranice komplexity: hledání řádu v chaotickém světě. Mladá fronta, Praha, 2003.
[E1] U. Eco: Foucaultovo kyvadlo. Odeon, Praha, 1991.
[E2] U. Eco: Hledání dokonalého jazyka. Nakladatelství Lidové noviny, Praha, 2001.
[FG] M. Field and M. Golubitsky: Symmetry in Chaos. A Search for Pattern in Mathematics, Art and Nature, Oxford University Press, Oxford, 1992.
[H] F. Harary: Graph Theory. Addison– Wesley, Reading, 1969.
[Kf] A. Kaufmann: Introduction a la combinatorique en vue des applications. Dunod, Paris, 1968.
[Km] E. Kamke: Differentialgleichungen reeler Funktionen. Akad. Verlaggessellschaft Geest und Portig K.-G., Leipzig, 1952.
[L] T. Leinkauf: Mundus combinatus. Studium zur Struktur der baroken Universalwissenschaft am Beispiel Athanasius Kircher S.J. (1602–1680), Akademie Verlag, Berlin, 1993.
[MRS] B. Müller, J. Reinhardt and M. T. Strickland: Neural Networks. An Introduction.
Springer, Berlin, 1995.
[Z] V. A. Zallgaller: Teoria ogibajuščich. Nauka, Moskva, 1975.

Tento text je rozšiřenou verzí článku, který je publikován v časopise Matematika, fyzika, informatika 14 (2004/2005).

01.04.2004